
Rule(s)
- Generics are the ability to express the behavior of a class by using anonymous types (a.k.a. “formal types”)
- Vocabulary: anonymous types are substituted by effective types when generics are put into practice.
Example Simple_genericity.Cpp.zip

// '.h' file: template <typename T> class LIFO { private: std::list<T> _representation; // '#include <list>' public: bool empty() const; void in(const T&); T out(); // This returns a copy! }; template <typename T> bool LIFO<T>::empty() const { return _representation.empty(); } template <typename T> T LIFO<T>::out() { if (empty()) throw "empty…"; T t = _representation.back(); _representation.pop_back(); return t; } template <typename T> void LIFO<T>::in(const T& t) { _representation.push_back(t); }// '.cpp' file: class Elephant { std::string _name; public: inline Elephant(std::string name) : _name(name) {} // 'inline' is for convenience only! inline std::string asString() const {return _name;} // 'inline' is for convenience only! }; int main(int argc, char** argv) { Elephant Babar("Babar"),Jumbo("Jumbo"); LIFO<Elephant> zoo; zoo.in(Babar); zoo.in(Jumbo); std::cout << "Jumbo goes out since it is the last-in: " << zoo.out().asString() << std::endl; return 0; }Rule(s)
- C++ Standard Template Library -STL- is rich enough of many generic classes, e.g.,
std::stack<T>.Example
#include <stack> … std::stack<char> stack_of_characters;Fundamentals
Default generic types and values
Rule(s)
- Default effective types or values may be defined using
=. At instantiation time, this allows us to avoid listing all effective types and values.- Template non-type parameters are substituted by values (instead of effective types) at instantiation time. A value has an integral or enumeration type. The type is pointer or reference to a class object, pointer or reference to a function, pointer or reference to a class member function or
std::nullptr_t.Example Heap.Cpp.zip

// At elaboration time: template<typename T,int default_capacity = 10,typename Default_representation = std::vector<T> > class Priority_queue { // '#include <vector>' private: Default_representation _representation; public: Priority_queue(int capacity = default_capacity) : capacity(capacity) { … // At instantiation time: Priority_queue<Task,100,std::deque<Task> > priority_queue; // '#include <deque>'Generic array
Rule(s)
- Generic arrays may be used instead of primitive arrays.
Example
std::vector<char> tab(2); // '#include <vector>' tab[0] = 'a'; tab[1] = 'b'; // tab[2] = 'c'; // Execution error: out of bounds tab.push_back('c'); // OK, capacity has automatically increasedExample
std::vector<std::string> sentence; // '#include <vector>' // Matrix of integers (caution: space required between '>' and '>'!): std::vector<std::vector<int> > matrix; // '#include <vector>'
std::array(C++11)Rule(s)
std::arraycumulates the benefit of primitive arrays (fixed sizes) along with the adaptability of STL containers.- Array overflow may be controlled (for reliability)… or not (for performance).
Example Palindrome.Cpp.zip

// '.h' file: class Palindrome : public std::string { … public: // Something less than '3' -> compilation "error: excess elements in struct initializer" constexpr static const std::array<char, 3> Special_characters{' ', '\n', '\t'}; … }; // '.cpp' file: const std::array<char, 3> Palindrome::Special_characters; … int out_of_bounds = Palindrome::Special_characters.size(); std::cout << Palindrome::Special_characters[out_of_bounds] << '\n'; // Out of bounds (no control)... try { std::cout << Palindrome::Special_characters.at(out_of_bounds) << '\n'; // Out of bounds (control)... } catch (std::logic_error& le) { // Inheritance graph: 'std::exception' < 'std::logic_error' < 'std::out_of_range' std::cerr << typeid(le).name() << ", " << le.what() << ": " << out_of_bounds << '\n'; }Generic functions
Rule(s)
- C++ lets developers the possibility of creating functions outside classes (this contrasts with a pure OO style). One may in particular create generic functions.
Example
template<typename T> void my_function(const T&); // Implementation occurs later... … char c; ::my_function(c); // Type inference avoids expanded form: '::my_function<char>(c);'Rule(s)
- For historical reasons, C++ offers a lot of predefined reusable and above all powerful generic functions. Their possible use occurs through
#include <algorithm>and#include <numeric>.Example
// Sorting: short tab[] = {13,7,6,4,12,11,8,3}; std::vector<short> vector(tab,tab + 8); for(int i = 0;i < vector.size();i++) std::cout << "-" << vector[i]; std::cout << std::endl; std::sort(vector.begin(),vector.end()); // #include <algorithm> for(int i = 0;i < vector.size();i++) std::cout << "-" << vector[i]; std::cout << std::endl; // Σ: std::cout << std::accumulate(vector.begin(),vector.end(),0) << std::endl; // #include <numeric>Mixing inheritance and generics
Rule(s)
- The mixing of inheritance and generics in C++ stumbles over natural (expected) contravariance problems.
Example Inheritance_and_genericity.Cpp.zip

// '.h' file: template <typename T> class Garden { private: // 'T' (as second anonymous type) acts as a functor (definition of 'operator()' required in 'T'): std::unordered_set <T, T> _garden; public: Garden(const T&); }; template <typename T> Garden<T>::Garden(const T& t) { _garden.insert(t); } class Vegetable { … }; class Cabbage : public Vegetable { … }; // '.cpp' file: Cabbage cabbage; Garden<Cabbage> garden(cabbage); // There is a risk to add carrots for instance, while 'another_garden' refers to a garden of cabbages only: // Garden<Vegetable>& another_garden = garden; // This *DOES NOT* work (contravariance)... Garden<Cabbage*> garden_(&cabbage); // There is a risk to add carrots for instance, while 'another_garden' refers to a garden of cabbages only: // Garden<Vegetable*>& another_garden_ = garden_; // This *DOES NOT* work (contravariance)...See also
Advanced features
Generic member function
Rule(s)
- As of Java, C++11 supports template member functions whose anonymous type(s) are totally independent of those of its enclosing class. Besides, the latter is not necessarily generic.
Example
class Any { public: template<typename Anonymous> void operator()(Anonymous&); };Specialization
Rule(s)
- Specialization amounts to substituting anonymous types by effective types along with, a priori, an altered behavior.
Example Advanced_genericity.Cpp.zip

// '.h' file: template<typename T> void my_function(T& t = std::declval<T>()) {T other = t;}; // Explicit specialization ('T' = 'int') -> *no default value for argument is permitted*: template<> void my_function(int& t) {int* other = &t;}; // Instantiation (declaration only since body presence means specialization!): template void my_function(char& t); // '.cpp' file: // (Incidental?) overload: void my_function(char& c) {std::cout << "'char& c' ver.: " << c << std::endl;}; … // ::my_function(); // Compilation error: 'candidate template ignored: couldn't infer template argument 'T'' char BEL = '\a'; ::my_function(BEL); // Existing overload preemption... ::my_function<char>(BEL); // Explicit instantiation ('T' = 'char') std::string a = "a"; // Or '::my_function<std::string>(a);': ::my_function(a); // Implicit instantiation ('T' = 'std::string')Template class specialization
Rule(s)
- Specialization of a template class also amounts to substituting anonymous types by effective types along with inheriting from something, having additional (member) attributes and/or functions, etc.
Example
// '.h' file: template<typename X> class Is_void : public std::false_type {}; // Base template // Specialization ('X' anonymous type is substituted for 'void' effective type): template</* Empty here! */> class Is_void<void> : public std::true_type {}; // '.cpp' file: std::cout << Is_void<char>::value << '\n'; // '0' meaning 'false' ('value' is a static field of both 'std::false_type' and 'std::true_type') // Implicit instantiation of specialization: std::cout << Is_void<void>::value << '\n'; // '1' meaning 'true'Alias template
Rule(s)
- From C++11 there is another way of dealing with
typedef.Example
template<typename X> using POINTER = X*; // Family of pointers of any type... template <typename T> void my_function(T t, POINTER<T> pt) { /* … */ }Example Heap.Cpp.zip

// '.h' file: template<typename E> using Heap_representation_size_type = typename E::size_type; template<typename T, int default_capacity = 10, typename Default_representation = std::vector<T> > class Priority_queue { … public: Heap_representation_size_type<Default_representation> count() const { return _representation.size(); } … }; // '.cpp' file: Priority_queue<Task, 100, std::deque<Task> > priority_queue; Task t1(1), t2(2), t3(3); priority_queue.insert(t1); priority_queue.insert(t2); priority_queue.insert(t3); Heap_representation_size_type<std::deque<Task> > count = priority_queue.count();Variable template (C++14)
Rule(s)
- Variables being non-member or member of classes may be made generic on their own.
Example Advanced_genericity.Cpp.zip

// 'constexpr' is for access at compilation time: template<typename Number> /* constexpr */ Number Mid = std::numeric_limits<Number>::max() - std::numeric_limits<Number>::min() / static_cast<Number> (2); template<typename My_anonymous> class My_class { public: // Declaration: template<class Number> static const Number Three_key_positive_values; static const My_anonymous My_class_property; // Non-template }; // Definition: template<typename My_anonymous> template<typename Number> const Number My_class<My_anonymous>::Three_key_positive_values = {std::numeric_limits<Number>::min(), Mid<Number>, std::numeric_limits<Number>::max()}; template<typename My_anonymous> const My_anonymous My_class<My_anonymous>::My_class_property = My_anonymous();Trailing return type
Rule(s)
- Generics benefit from the concomitant use of the
decltypeoperator. In template functions especially, the principle of “trailing return type” is the fact the function's returned type depends upon parameter(s)' type(s).Example Constexpr.Cpp.zip

// This requires the explicit introduction of 'Result' at instantiation time: template<typename T, typename Result> Result multiply(T t1, T t2) { return t1 * t2; } // Compiler fails because 't1' and 't2' are undefined (left-to-right parsing): // template<typename T> decltype(t1 * t2) multiply(T t1, T t2) { // decltype(t1 * t2) t = t1 * t2; // This works here only... // return t; //} // Trailing return type thanks to 'auto': template<typename T> /* [] */ auto multiply(T t1, T t2) -> decltype(t1 * t2) { return t1 * t2; }
Rule(s)
- Standard Template Library -STL- is for many years fully part of C++ while it initially was an external library. STL is mainly constituted of “container” classes, i.e., “collections”, but it also includes generic algorithms that may be found in
<algorithm>and in<numeric>.Generic algorithms
std::accumulatestd::binary_searchstd::findstd::for_eachstd::make_heapstd::reversestd::set_differencestd::set_intersectionstd::sortstd::sort_heapstd::transform- Etc.
Generic algorithms in practice
Specification
E ⊂ F ⇔ E ⊆ F ∧ E ≠ F. This leads to:strict_subset? (i.e., ⊂): My_set x My_set -> Boolean with s1, s2: My_set, strict_subset?(s1,s2) = subset?(s1,s2) ∧ ∼equals?(s1,s2)E - F = {t ∈ E ∧ t ∉ F}. This leads to:difference: My_set x My_set -> My_set with s1, s2: My_set, ti: T, difference(s1,s2) = [remove(union(s1,s2),ti)]belongs?(ti,s2)Implementation
Example List_map_set.Cpp.zip

template <typename T> class My_set : public std::set<T> { // Inheritance public: bool strict_subset(const My_set<T>&); My_set<T> operator -(const My_set<T>&); }; template<typename T> bool My_set<T>::strict_subset(const My_set<T>& s) { My_set<T> intersection; std::set_intersection(this->begin(),this->end(),s.begin(),s.end(),std::inserter(intersection,intersection.end())); return intersection == *this && intersection != s; } template<typename T> My_set<T> My_set<T>::operator -(const My_set<T>& s) { My_set<T> difference; std::set_difference(this->begin(),this->end(),s.begin(),s.end(),std::inserter(difference,difference.end())); return difference; }
Rule(s)
- C++ sequences offer key facilities over native arrays. Typically, the
std::vector<T>class owns thepush_backfunction, which automatically expands the capacity of arrays while native arrays have to be manually reallocated by means of thedelete[]andnewC++ operators.Example
// '.h' file: class Prisoner { … std::list<const Criminal_case*> _all_criminal_cases; … // '.cpp' file: // Adding at the end: void Prisoner::involve(const Criminal_case& criminal_case) { _all_criminal_cases.push_back(&criminal_case); } // First alternative, adding at the beginning: void Prisoner::involve(const Criminal_case& criminal_case) { _all_criminal_cases.push_front(&criminal_case); } // Getting the last one: const Criminal_case* Prisoner::last() const { return _all_criminal_cases.empty() ? NULL : _all_criminal_cases.back(); }C++ sequences
std::array<T,N> // '#include <array>'std::deque<T,Alloc> // '#include <deque>'std::queue<T,Container> // '#include <queue>'std::stack<T,Container> // '#include <stack>'std::vector<T,Alloc> // '#include <vector>'- Etc.
Example (
std::dequeversusstd::queue)std::deque<char> my_deque; my_deque.push_back('O'); my_deque.push_back('K'); my_deque.push_front('K'); my_deque.pop_back(); for (auto c : my_deque) // 'KO' is displayed std::cout << c; std::cout << std::endl; std::queue<char, std::list<char> > my_queue; // List as backbone... my_queue.push('K'); my_queue.push('O'); my_queue.push('K'); my_queue.pop(); for (auto c : my_deque) // 'KO' is displayed std::cout << c; std::cout << std::endl;
Rule(s)
- C++ sets are accessible via the
#include <set>or#include <unordered_set>macro-statements.
std::setRule(s)
- Former C++ sets in STL by default use the
std::less<T>class as duplicate discriminator. Beyond, insertions maintain an order based on this discriminator.Example List_map_set.Cpp.zip

std::set<char> alphabet; // This is equivalent to: 'std::set<char,std::less<char> > alphabet;' alphabet.insert('a'); alphabet.insert('a'); // Without effect because 'a' < 'a' is 'false' assert(alphabet.size() == 1);Alternative (this requires the redefinition of the
>operator in theTaskclass)std::set<Task,std::greater<Task> > scheduler;Creating sets from native arrays and searching in sets
short tab[] = {3,4,6,7,8,11,12,13}; std::set<short> set(tab,tab + 8); assert(std::binary_search(set.begin(),set.end(),13)); // '#include <algorithm>' assert(! std::binary_search(set.begin(),set.end(),14)); // '#include <algorithm>'
std::unordered_set(C++11)Rule(s)
- Latter C++ sets in STL do not maintain any order and rely on a “true” hash method for object storage in sets.
Memory management principle
A reserved memory area offers storage positions and related indices. For a to-be-stored object, a position is computed through a hash method. Position matches to an index in the memory area (modulo memory area capacity). Conflict resolution (i.e.,
position(o1) == position(o2)) leads to two scenarios:
- if
o1 == o2then erasure, i.e.,o2eraseso1in the memory area (o2is inserted aftero1).- if
o1 != o2then some strategies of conflict resolution sketched in figure allow the storage of botho2ando1at the “same” position (a.k.a. “bucket”: typicallystd::listin C++). As a result, usingstd::unordered_setinvolves, beyond a hash method, the definition of==operator in order to computeo1 == o2.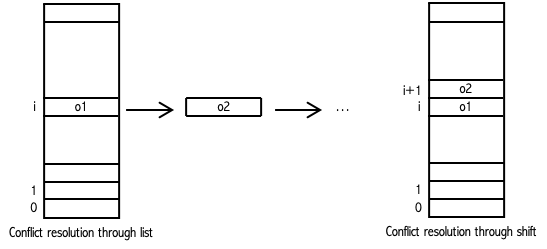
Formally, efficiency (insertion, search…) relies on position computation efficiency. Complexity is
O(1)- constant, evenO(n)- linear in the worst case.Example Inheritance_and_genericity.Cpp.zip

// '.h' file: template <typename T> class Garden { private: // 'T' (as second anonymous type) acts as a functor (definition of 'operator()' required in 'T'): std::unordered_set <T, T> _garden; public: Garden(const T&); }; template <typename T> Garden<T>::Garden(const T& t) { _garden.insert(t); } class Vegetable { // Abstract class, 'operator==' is defined in subclasses... public: std::size_t operator()(const Vegetable& vegetable) const { // Hash on several fields uses '^': https://www.techiedelight.com/use-pair-key-std-unordered_set-cpp/ std::hash<std::bitset<sizeof (Vegetable*)> > hash; return hash(reinterpret_cast<uintptr_t> (&vegetable)); // Storage relies on memory address! } … }; class Cabbage : public Vegetable { … }; // 'operator==' is defined here... // '.cpp' file: Garden<Cabbage> garden(cabbage{});C++ allows a fine-grain control of the way the memory area is initially reserved (capacity at construction time) and intended to be used (load factor). Any ill-formed memory area may lead to many conflict resolutions, which themselves lead to space and time overheads. Real-time re-organization of the underlying memory area is possible (but in essence shaky) through specific member functions:
max_load_factor,reserve, etc.
Rule(s)
- Maps are also named “associative containers”, “dictionaries”, or “hash tables” in the sense that data inside maps are pairs of keys and values. Keys are by construction organized as a set.
- C++ maps are accessible via the
#include <map>macro-statement for common maps including multi-maps. Multi-maps allow multiple values for the same key.- From C++11, unordered maps and unordered multi-maps have been introduced (
#include <unordered_map>).Why maps?
Examples (how to represent the
5x2 - 3x + 8polynomial without maps?)double polynomial[] = {8.,-3.,5.} // First possibility… -> bad ideaAlternative
std::list<std::pair<int,double> > polynomial; // Second possibility… -> fairly bad ideaExample (how to represent the
8x39 - 12x10polynomial with maps?)std::map<int,double> polynomial; polynomial[39] = 8.; polynomial[10] = -12.;Ordered maps
Rule(s)
- There is not “true” position computation. By default, as ordered sets,
std::less<T>is used to get storage indices from keys.- C++ (default) conflict management:
!(k1 < k2) && !(k2 < k1)⇔k1andk2are “the same key”. Namely, for string objects as keys (shown in example below):!(s1 < s2) && !(s2 < s1)⇔s1ands2are “the same key”. String objects are compared and therefore stored usingstd::less<std::string>.Example (unshared key)
// Equivalent to 'std::map<std::string,std::string,std::less<std::string> > given_names__dictionary;': std::map<std::string,std::string> given_names__dictionary; std::string s1 = "Franck";
std::string s2 = "Franck";
given_names__dictionary[s1] = "English origin given name"; // This value is going to be lost... given_names__dictionary[s2] = "German origin given name"); assert(given_names__dictionary.size() == 1);Example (shared key, i.e., multi-maps)
std::multimap<std::string,std::string> given_names__dictionary; std::string s1 = "Franck"; std::string s2 = "Franck"; given_names__dictionary[s1] = "English origin given name"; // This value is *NOT* going to be lost... given_names__dictionary[s2] = "German origin given name"); assert(given_names__dictionary.size() == 2);Exercise
Implement Horner's method here…, which is an efficient mechanism to evaluate a polynomial for a
xvariable. Horner's method principle is the factorization ofxso that prior iteration result is multiplied byx. Related coefficient ofxis added during iteration.#ifndef _Horner_h #define _Horner_h #include <initializer_list> #include <map> #include <string> class Polynomial { private: std::map<unsigned, double> _representation; public: Polynomial(const std::initializer_list<std::map<unsigned, double>::value_type>&); double horner_method(const double) const; double simple_method(const double) const; std::string toString() const; }; #endifHorner's method singles out an order of monomials from higher to lower powers of
x. Difficulty resides in powers ofxthat are absent.
- Copy/paste and test program
- Next, complete line 20 with appropriate code
#include <cmath> #include <initializer_list> #include <iostream> #include <map> #include <stdexcept> #include <string> #include "Horner.h" Polynomial::Polynomial(const std::initializer_list<std::map<unsigned, double>::value_type>& monomials) { for (std::map<unsigned, double>::value_type monomial : monomials) // "Range-based 'for'" _representation.insert(monomial); } double Polynomial::horner_method(const double x) const { double result = 0; // Existing (descending) order of powers of 'x': // for (std::map<unsigned, double>::const_reverse_iterator i = _representation.rbegin(); i != _representation.rend(); i++) std::cout << (*i).first << " - "; return result; } double Polynomial::simple_method(const double x) const { double result = 0; for (auto& [key, value] : _representation) result += value * ::pow(x, (double)key); return result; } std::string Polynomial::toString() const { std::string result; for (auto& [key, value] : _representation) result += std::to_string(value) + " * x^^" + std::to_string(key) + " + "; return result.substr(0, result.size() - 3); } int main(int argc, char** argv) { Polynomial p({ {4U,3.},{2U,2.},{0U,1.} }); std::cout << p.toString() << std::endl; std::cout << "Horner method(2.): " << p.horner_method(2.) << std::endl << std::endl;; return 0; }Application(s)
Unordered maps
Rules
- Unordered maps allow quicker insertion since no order is kept. Search relies on a “true” hash method (i.e., position computation) instead of keys' order in common maps. As a result, performance differences exist between ordered and unordered maps; they are described here…
- C++ provides predefined hash functions for primitive types like
intfor instance, built-in types as well, notablystd::string. Hash functions rely on complex mathematics/statistics and, a priori, are compiler-dependent.Example (unordered map) Polynomial.Cpp.zip

#ifndef _POLYNOMIAL_H #define _POLYNOMIAL_H #include <cstddef> // 'std::size_t' #include <unordered_map> class Polynomial { private: std::unordered_map<int, double> _representation; public: Polynomial(const std::initializer_list<std::unordered_map<int, double>::value_type>&); const Polynomial& operator=(const Polynomial&); // No value, for illustration only, make underlying default hash function (keys are powers of 'x', i.e., integers) explicit: std::size_t hashCode(const std::unordered_map<int, double>::key_type&) const; // Java style! }; #endif /* _POLYNOMIAL_H */#include <algorithm> // 'std::copy'... #include <iostream> #include <iterator> // 'std::inserter'... #include "Polynomial.h" Polynomial::Polynomial(const std::initializer_list<std::unordered_map<int, double>::value_type>& members) { _representation.insert(members); // for (std::unordered_map<int, double>::value_type member : members) _representation.insert(member); } const Polynomial& Polynomial::operator=(const Polynomial& p) { if (this != &p) { _representation.clear(); std::copy(p._representation.begin(), p._representation.end(), std::inserter(_representation, _representation.begin())); } return *this; } std::size_t Polynomial::hashCode(const std::unordered_map<int, double>::key_type& key) const { // Get default hash function: std::unordered_map<int, double>::hasher hash = _representation.hash_function(); return hash(key); } int main(int argc, char** argv) { Polynomial p{ {39, 8.},{10, -12.} }, q{ {1, 1.} }; q = p; std::cout << "Hash of '39': " << p.hashCode(39) << std::endl; std::cout << "Hash of '10': " << p.hashCode(10) << std::endl; return 0; }Rule(s)
- C++ predefined (reusable) hash functions strictly respect the following formal rule:
o1 == o2 ⇒ hash(o1) == hash(o2), i.e.,hash(o1) != hash(o2) ⇒ o1 != o2.- Note that
o1 != o2 ⇒ hash(o1) != hash(o2)is “highly expected”, but non mandatory, to, as much as possible, avoid conflicts.- Tailor-made hash functions may be introduced with great care as done in exercise below. Special attention should be paid to prior formal rule.
Exercise
EAN-13 here is a European 13-digit format (bar code) for products. The following C++ program puts forward a notion of product database (
EAN_13_databaseclass). Each product database records products based on a unordered map (_representationattribute) whose keys areEAN_13objects and values are images.The C++ program reuses the hash function (within the
_EAN_13_keyclass) of thestd::string_viewtype from C++17. Note that the==operator inEAN_13is contextually defined in strict relation with the way, the hash function operates in_EAN_13_key.#ifndef _EAN_13_h #define _EAN_13_h #include <array> // 'std::to_array' from C++20 (https://en.cppreference.com/w/cpp/container/array/to_array) #include <bitset> #include <initializer_list> #include <stdexcept> #include <string_view> // 'std::hash' for string view objects... #include <unordered_map> class EAN_13 { // 'EAN_13' objects act as keys in unordered maps... private: // https://www.codesdope.com/cpp-stdarray (warning: 'std::array 'size is defined at compilation time!) std::array<char, 13> _representation{}; // '{}' => The 13 digits are set to '\0' character... public: EAN_13(const std::initializer_list<char>&); // Key computation (hash) requires contextual definition of '==' operator: bool operator==(const EAN_13&) const; std::string_view toString() const; // 'std::string_view' from C++17 (https://www.safetica.com/blog/do-you-know-std-string_view-and-how-to-use-it) }; class _EAN_13_key { public: // Key computation (hash) requires contextual definition of '()' operator: std::size_t operator()(const EAN_13&) const noexcept; }; class EAN_13_database { private: // Third parameter is the hash function: std::unordered_map<EAN_13, std::bitset<4096>, _EAN_13_key> _representation; // As an illustration, values may be images of 16x16 grayed pixels without alpha... public: EAN_13_database(const std::initializer_list<EAN_13>&); inline std::size_t size() const { return _representation.size(); } }; #endifThe C++ program reuses the hash function of the
std::string_viewtype from C++17, but analysis shows that the call totoString(line 30, below) at each key computation can be considered as non-optimal.Copy/paste and test program. Next, address possible sub-optimality (tip: explore
remove_suffixinstance function here… ofstd::string_viewtype).#include <cassert> #include <cstring> // '::strncpy' #include <iostream> #include "EAN_13.h" // 'std::array' has no constructor; '_representation(digits)' won't work... EAN_13::EAN_13(const std::initializer_list<char>& digits) /*: _representation(digits)*/ { std::array<char, 13>::iterator j = _representation.begin(); for (std::initializer_list<char>::const_iterator i = digits.begin(); !(i == digits.end()); i++, j++) *j = *i; } bool EAN_13::operator==(const EAN_13& product) const { return _representation == product._representation; // 'std::array' supports '==' (https://en.cppreference.com/w/cpp/container/array/operator_cmp) } std::string_view EAN_13::toString() const { const char* data = this->_representation.data(); // Primitive underlying array *WITHOUT* '\0'! /** Back to middle age */ char buffer[13 + 1]; buffer[13] = '\0'; ::strncpy(buffer, data, 13); /** End of "back to middle age" */ std::string_view sv(buffer); // 'std::string_view' avoids copy here... return sv; } std::size_t _EAN_13_key::operator()(const EAN_13& product) const noexcept { // Robustness invites us to reuse key computation based on string view objects: return std::hash<std::string_view>{}(product.toString()); } EAN_13_database::EAN_13_database(const std::initializer_list<EAN_13>& products) { for (EAN_13 product : products) _representation[product] = std::bitset<4096>{}; } int main(int argc, char** argv) { // 471-9-5120-0288-9 EAN_13 product{ {'4','7','1','9','5','1','2','0','0','2','8','8','9'} }; // std::cout << "EAN-13 product: " << product.toString() << std::endl; EAN_13 product_{ {'4','7','1','9','5','1','2','0','0','2','8','8','9'} }; // Same data in memory... EAN_13_database database({ product,product_ }); assert(database.size() == 1); return 0; }Application(s)
Example List_map_set.Cpp.zip

std::list<const Task*> l; assert(l.empty()); l.push_front(&t1); // t1 l.push_front(&t2); // t2 t1 l.push_front(&t3); // t3 t2 t1 l.push_front(&t4); // t4 t3 t2 t1 l.insert(l.begin(), &t5); // t5 t4 t3 t2 t1 l.push_back(&t1); // t5 t4 t3 t2 t1 t1 assert(l.size() == 6); std::list<const Task*>::iterator j; for (j = l.begin(); !(j == l.end()); j++) std::cout << "- " << (*j)->start() << '\t'; std::list<const Task*>::iterator where_is_t2 = std::find(l.begin(), l.end(), &t2); std::cout << "Task 't2': " << (*where_is_t2)->start() << std::endl; std::reverse(l.rbegin(), l.rend()); // t1 t1 t2 t3 t4 t5 for (j = l.begin(); !(j == l.end()); j++) std::cout << "- " << (*j)->start() << '\t'; std::list<const Task*>::reverse_iterator k; for (k = l.rbegin(); !(k == l.rend()); k++) std::cout << "- " << (*k)->start() << '\t'; l.sort(); // Pointers order: t5 t4 t3 t2 t1 t1 for (j = l.begin(); !(j == l.end()); j++) std::cout << "- " << (*j)->start() << '\t'; l.unique(); // t5 t4 t3 t2 t1 (remove only consecutive elements?) for (j = l.begin(); !(j == l.end()); j++) std::cout << "- " << (*j)->start() << '\t';
for loopRule(s)
- C++11 comes with a simplified possibility of iterating on collections without the explicit introduction of “cursors” like iterators.
Example
for (char c : my_string) { // 'my_string' has 'std::string' type…Rule(s)
- Range-based
forloop may be used with C++17 binding as well.Example
std::unordered_multimap<std::string, std::string> oscars_2024_best_actress { {"Emma Stone", "Winner"}, {"Lily Gladstone", "Nominee"}, {"Annette Bening", "Nominee"}, {"Carey Mulligan", "Nominee"}, {"Sandra Hüller", "Nominee"}}; for (auto&& [name, status] : oscars_2024_best_actress) // Binding (C++17) std::cout << name << " as " << status << std::endl;See also
Even though
std::_Rb_treeis a native STL generic class, it does not aim ('_' sign just before “Rb_tree”) at being reused in a direct way. Instead, most STL collections have red-black tree data structures as backbones likestd::set<Key,Compare,Allocator>.Rule(s) as invariants
- Root is black
- If a node is red then left and right sons are black; missing son means black
- Any path from a node to a leaf has the same number of black nodes (a.k.a. “tree's black height”); a red-black tree is then approximately balanced
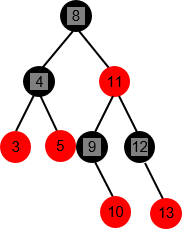
Example (homemade red-black tree)
#ifndef _Red_black_tree #define _Red_black_tree #include <cstddef> // 'NULL' #include <list> using namespace std; template <typename T> class Red_black_tree { private: list<Red_black_tree<T>*> garbage_collector; T _content; Red_black_tree<T>* _left, * _right, * _super; enum { red, black } _color; void balance(Red_black_tree<T>*, const Red_black_tree<T>* const); void insert(const T&, const Red_black_tree<T>* const); void left_rotate(); void right_rotate(); public: Red_black_tree(const T&); ~Red_black_tree(); void insert(const T&); }; template <typename T> void Red_black_tree<T>::balance(Red_black_tree<T>* rbt, const Red_black_tree<T>* const root) { if (rbt->_super == root) { rbt->_color = black; return; } while (rbt->_super->_color == red) { if (rbt->_super == rbt->_super->_super->_left) { Red_black_tree* y = rbt->_super->_super->_right; if (y && y->_color == red) { rbt->_super->_color = black; y->_color = black; rbt->_super->_super->_color = red; rbt = rbt->_super->_super; } else { if (rbt == rbt->_super->_right) { rbt = rbt->_super; rbt->left_rotate(); } rbt->_super->_color = black; rbt->_super->_super->_color = red; rbt->_super->_super->right_rotate(); } } else { Red_black_tree* y = rbt->_super->_super->_left; if (y && y->_color == red) { rbt->_super->_color = black; y->_color = black; rbt->_super->_super->_color = red; rbt = rbt->_super->_super; } else { if (rbt == rbt->_super->_left) { rbt = rbt->_super; rbt->right_rotate(); } rbt->_super->_color = black; rbt->_super->_super->_color = red; rbt->_super->_super->left_rotate(); } } } } template <typename T> void Red_black_tree<T>::insert(const T& t, const Red_black_tree<T>* const root) { if (_content < t) { if (!_right) { _right = new Red_black_tree<T>(t); _right->_super = this; garbage_collector.push_back(_right); balance(_right, root); } else _right->insert(t, root); } else { if (!_left) { _left = new Red_black_tree<T>(t); _left->_super = this; garbage_collector.push_back(_left); balance(_left, root); } else _left->insert(t, root); } } template <typename T> void Red_black_tree<T>::left_rotate() { if (!_right) return; Red_black_tree<T>* temp = _right; if (_right->_left) _right->_left->_super = this; _right = _right->_left; temp->_left = this; Red_black_tree<T>* pseudo_root = this->_super; this->_super = temp; temp->_super = pseudo_root; if (pseudo_root->_left == this) pseudo_root->_left = temp; else pseudo_root->_right = temp; } template <typename T> void Red_black_tree<T>::right_rotate() { if (!_left) return; Red_black_tree<T>* temp = _left; if (_left->_right) _left->_right->_super = this; _left = _left->_right; temp->_right = this; Red_black_tree<T>* pseudo_root = this->_super; this->_super = temp; temp->_super = pseudo_root; if (pseudo_root->_left == this) pseudo_root->_left = temp; else pseudo_root->_right = temp; } template <typename T> Red_black_tree<T>::Red_black_tree(const T& t) : _content(t) { _left = _right = _super = NULL; _color = red; } template <typename T> Red_black_tree<T>::~Red_black_tree() { typename list<Red_black_tree<T>*>::iterator i; for (i = garbage_collector.begin(); i != garbage_collector.end(); i++) delete* i; } template <typename T> void Red_black_tree<T>::insert(const T& t) { if (_content < t) { if (!_right) { _right = new Red_black_tree<T>(t); _right->_super = this; garbage_collector.push_back(_right); balance(_right, this); } else _right->insert(t, this); } else { if (!_left) { _left = new Red_black_tree<T>(t); _left->_super = this; garbage_collector.push_back(_left); balance(_left, this); } else _left->insert(t, this); } _color = black; } #endifRule(s)
- Complexity of insertion, search and suppression is
O(log(n))- logarithmic. These three public operations rely on three private operations (left-rotate, right-rotate and balance) to hold invariants.Example (insertion of
9)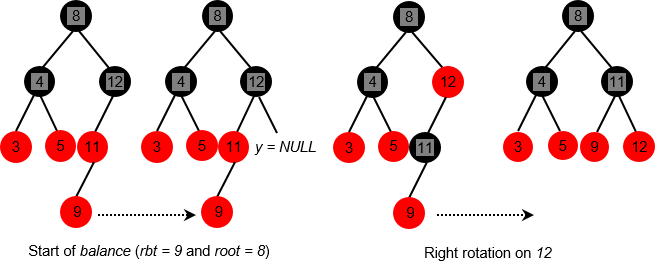
#include "Red_black_tree.h" int main() { Red_black_tree<int> rbt(8); rbt.insert(5); rbt.insert(4); rbt.insert(12); rbt.insert(3); rbt.insert(11); rbt.insert(9); rbt.insert(13); rbt.insert(10); return 0; }Application(s)
There no direct graph and graph algorithm supports in C++ apart from reusing third-party (focused) libraries. However, the power of STL allows numerous and varied representations of graphs based on standard containers.
Example (directed graph based on
std::unordered_multimap)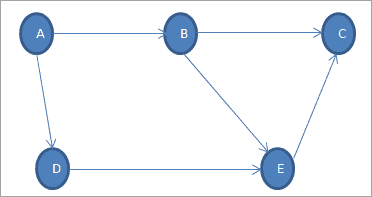
#ifndef _DIRECTED_GRAPH_h #define _DIRECTED_GRAPH_h #include <initializer_list> #include <stdexcept> #include <string> #include <unordered_map> #include <unordered_set> #include <utility> // 'std::pair' class Node { public: const std::string name; Node(const std::string&); bool operator==(const Node&) const; // Distinction is based on 'name'... }; class _Node_key { public: std::size_t operator()(const Node&) const noexcept; // Hash function based on 'name'... }; class Directed_graph { private: // Edges: A->B, A->D, B->C, B->E, D->E, E->C and possible C->D cycle std::unordered_multimap<const Node, const Node, _Node_key> _representation; // (A->(B,C),(B->(C,E)),(D->(E)),(E->(C)) and possible (C->(D)) cycle bool _cyclic_(const Node&, std::pair<std::list<std::pair<const Node, const Node> >::const_iterator, std::list<std::pair<const Node, const Node> >::const_iterator>&, const std::unordered_set<Node, _Node_key>&, int&) const; public: Directed_graph(const std::initializer_list<std::unordered_multimap<const Node, const Node, _Node_key>::value_type>&); bool acyclic_() const; inline std::size_t size() const { return _representation.size(); } }; #endif#include <iostream> #include <ranges> // Unused... #include "Directed_graph.h" Node::Node(const std::string& name) : name(name) {} bool Node::operator==(const Node& node) const { return name == node.name; } std::size_t _Node_key::operator()(const Node& node) const noexcept { return std::hash<std::string>{}(node.name); // Empty curly braces creates an object to instrument the call of '()' operator... } Directed_graph::Directed_graph(const std::initializer_list<std::unordered_multimap<const Node, const Node, _Node_key>::value_type>& edges) { for (auto& [edge_origin, edge_destination] : edges) { // C++17 structural bindings... auto range = _representation.equal_range(edge_origin); // All destinations from 'edge_origin'... auto addition = true; for (auto& i = range.first; addition && i != range.second; i++) if (edge_destination == (*i).second) addition = false; // Avoid 2 or several times, for instance, A->B if (addition) _representation.insert(std::make_pair(edge_origin, edge_destination)); // A->B, A->D, Etc. } } bool Directed_graph::_cyclic_(const Node& from, std::pair<std::list<std::pair<const Node, const Node> >::const_iterator, std::list<std::pair<const Node, const Node> >::const_iterator >& outgoing_edges, const std::unordered_set<Node, _Node_key>& edge_origins, int& cost) const { for (auto& i = outgoing_edges.first; i != outgoing_edges.second; i++) { // from = A *** outgoing_edges = {(A->B),(A->D} if (from == (*i).second) return true; // Loop like A->A // if (edge_origins.contains((*i).second)) { // C++20 only... if (edge_origins.find((*i).second) == edge_origins.end()) { // If B in 'edge_origins' then don't explore from A because A->B... auto outgoing_edges = _representation.equal_range((*i).second); cost++; if (_cyclic_(from, outgoing_edges, edge_origins, cost)) return true; // If at least one cycle found then graph isn't acyclic... } } return false; // No cycle found yet... } bool Directed_graph::acyclic_() const { // If edges have the same origin then get origin once: std::unordered_set<Node, _Node_key> edge_origins; for (auto& [edge_origin, edge_destination] : _representation) edge_origins.insert(edge_origin); // std::list<Node> edge_origins; // std::ranges::copy(std::views::keys(_representation), std::back_inserter(edge_origins)); // C++20 // Alternative with pipe syntax from C++20: // std::ranges::copy(_representation | std::views::keys, std::back_inserter(edge_origins)); // edge_origins.unique(); // Non-robust because only *CONSECUTIVE* duplicates are removed... int cost = 0; for (auto& edge_origin : edge_origins) { // Explore graph from nodes as edge origins... auto edge_destinations = _representation.equal_range(edge_origin); // e.g., values of A key -> (B,C) if (_cyclic_(edge_origin, edge_destinations, edge_origins, cost)) return false; // If at least one cycle found then graph isn't acyclic... } return cost != 0; } int main(int argc, char** argv) { const Node a("A"), b("B"), c("C"), d("D"), e("E"); Directed_graph directed_graph({ /*std::make_pair(a, a),*/std::make_pair(a, b),std::make_pair(a, b),std::make_pair(a, d), std::make_pair(b, c),std::make_pair(b,e), std::make_pair(d, e),std::make_pair(e, c),/*std::make_pair(c, d)*/ }); // std::cout << "'directed_graph.size()': " << directed_graph.size() << std::endl; std::cout << "Is 'directed_graph' acyclic? " << (directed_graph.acyclic_() ? "YES" : "NO") << std::endl; return 0; }Exercise (implement the two following
Directed_graphmember functions)// Tip: 'std::set_intersection' between keys and values... std::unordered_set<Node, _Node_key> leafs() const; // Nodes without any outgoing edge... std::unordered_set<Node, _Node_key> roots() const; // Node without any incoming edge...Application(s)